Sat Solver, Part 2

Due: Wed Oct 09 11:59 pm
Starter files: lab5.zip
Submission: Please submit your work using Gradescope.

Overview

In this lab, you will continue to work on the SatSolver from lab4. The goal is to optimize your implementation so it runs fast and makes as few recursive calls as possible.

Your final grade will be based on two factors:

Correctness: your speedy implementation must pass all the tests from the previous lab.
Speed/search cost: to receive full credit, you must implement at least one of the optimizations below. I will use a benchmark to gauge how effectively the optimization was implemented.

Contest

Through Gradescope, I will run a contest comparing all implementations on a benchmark of satisfiability problems (see below).

Top performers will win a prize!

Solver Benchmark

Your implementation will be run through a benchmark, provided in SolverBenchmark. The benchmark runs your code on a bunch of randomly generated propositions and it records the time and number of recursive calls made.

The benchmark is based on this famous scientific discovery. In 1994, researchers learned two important properties about CNF propositions. These insights were reported in Science, the most prestiguous venue for scientific research. First, they found that the likelihood that a proposition is satisfiable depends on the ratio between number of clauses and number of variables. When the ratio is less than 4, almost all propositions are satisfiable; when the ration is above 5, almost all are unsatisfiable. Second, they found that the hardest propositions to check lie between 4 and 5. Understanding “where the hard problems are” is of great theoretical and practical value.

The SolverBenchmark approximately replicates their experiment. Here are the results from my implementation. (I modified the benchmark to get more data points, but the idea is the same.)

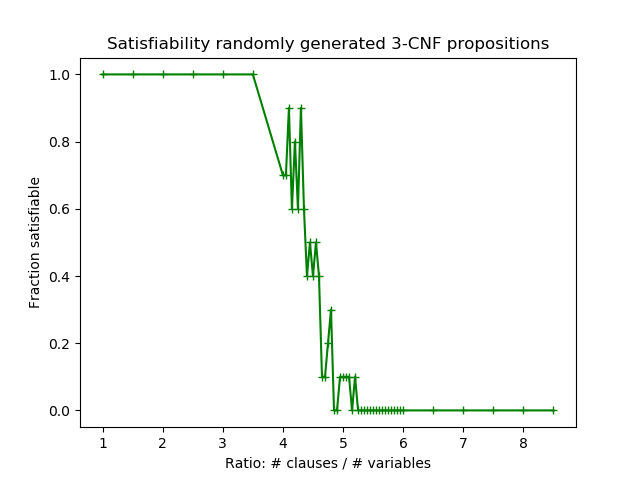
Figure of results on satisfiability

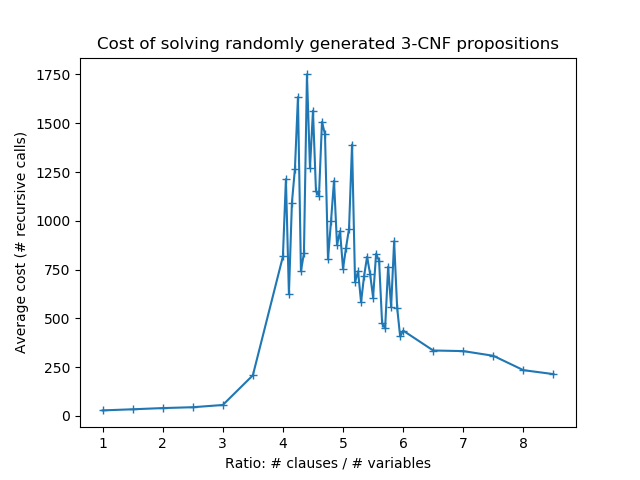
Figure of results on search cost

Optimizations

Here are some potential optimizations you might consider.

Optimization 1: Stop early

It may not be necessary to assign every variable a value to determine whether the current model leads to satisfiable assignment.

For example, suppose $\varphi := (p \lor q) \land (p \lor r) \land (p \lor s)$ and model $M$ has assigned $p$ to true. In this case, $\varphi$ is satisfiable regardless of how $q$ $r$, or $s$ are assigned.

Another example, suppose $\varphi := (p) \land (q \lor r) \land (s \lor \lnot q) \land (t \lor r) \land (\lnot q \lor t)$ and model $M$ has assigned $p$ to false. In this case, $\varphi$ is unsatisfiable under model $M$ regardless of how $q$, $r$, $s$, $t$ are assigned.

A final example, suppose $\varphi := (\lnot p \lor q) \land (\lnot p \lor r)$ and model $M$ has assigned $p$ to true. In this case, we do not know yet whether $\varphi$ is unsatisfiable. It might be or it might not be: it depends on how $q$ and $r$ are assigned.

Thus, the optimization is this:

when the current model assignment makes every clause true, stop early and return true.
when the current model assignment makes at least one clause false, stop early and return false.

Optimization 2: Choose variables in undetermined clauses

Continuing the idea started with optimization 1, when choosing a variable, we might focus on variables that appear in clauses that are not already true according to the current assignment.

For example, suppose $\varphi := (p \lor q \lor t) \land (\lnot p \lor s)$ and model $M$ has assigned $p$ to true. In this case, the first clause is already true and we should focuse on the second clause and choose $s$.

Optimization 3: Choose a pure variable

A pure variable is one that always appears as a positive, or always appears negative. Pure variables are easy: if the variable is positive, it must be assigned true if the proposition is satisfiable; if the variable is always negative, it must be assigned false.

Note that an impure variable can become pure under a model: For example, in the proposition $(p \lor q) \land (p \lor r) \land (\lnot p \lor s)$ when $s$ is true, then we can ignore the last clause ($s$ being True, makes the last clause true) and so $p$ becomes pure and it must be assigned to true.

Optimization 4: Choose unit clause variables

A unit clause variable is a variable that appears by itself in a clause. For example, in the proposition, $(\lnot p) \land (p \lor q)$, variable $p$ is in a unit clause. Like with pure variables, a variable in a unit clause must be assigned a certain truth value (in the example $p$ must be false).

Also like pure variables, a clause can become a unit clause under a model. For example if the proposition is $(p \lor q \lor \lnot r)$ and $q$ is assigned false and $r$ is assigned true, then $p$ becomes a unit clause variable.

If you implement this along with optimization 3, you might choose unit clause variables should be considered only after all pure variables have been assigned.

Bonus challenge problem

Here’s an additional challenge problem, worth a bit more extra credit. The task is to design and implement an efficient algoritm for sat solving. By efficient, I mean that the runtime is proportional to some function that is polynomial in the size of the input. If you complete this, and can prove that the algorithm is correct and that the runtime is polynomial, you will be rewarded with $1 million.